Explain the Output or End Product of Gaussian Elimination
Learn more about matlab function gaussian elimination linear algebra for loop. The end product of Gauss Jordan elimination is a matrix in reduced row echelon form.

Solved Consider The Following System Of Linear Equations B 0 Chegg Com
Example 1 Solve each of the following systems of equations.
. Implementation of the Gaussian elimination algorithm over GF2 more generally over GFp on systolic com- puting systems and in VLSI has been considered by several researchers. 4x 3y 11 x 3y 1. In eliminating columnj we do nj2multiplies and the same number of subtractions.
Systolic algorithms for Gaussian elimination of dense. Inverse of an invertible square matrix. Rewrite the matrix equation as a homogeneous system of linear equations and solve the homogeneous linear system.
The function should perform Gaussian elimination row reduction to reduce Alb to row echelon form. C 1 2 -1. Q 1 T v 3 q 2 T v 3 0 q 1 T v 3 0 δ δ.
The input A is a square matrix and the outputs are the lower triangular matrix L and the upper triangular matrix U in the LU factorization of A. Since δ is very small δ 2 is much smaller. We can also apply Gaussian Elimination for calculating.
Solving AxB using Gaussian. 4 1 33. Once we have the augmented matrix in this form we are done.
Output x2 05X2 We The dot product of two vectors and in is defined by Y2 320 Industry 13 output x3 150. Rank of a matrix. This method is called Gauss-Jordan Elimination.
So in all the number of multiplies and adds is n1 j1 nj2 n1 k1 k 1 6 n3On2 Bindel Spring 2022 Numerical Analysis We also performOn2 divisions. 19 R R E i j α E i j α 1 The reverse of the previous sequence allows one to perform Gaussian elimination in the lines of suitable correct dimensions and the sequence of elementary transformations achieves the desired row. 1 Solve the given system by Gaussian elimination.
Suppose you apply GaussJordan elimination to a matrix. Explain how you can be sure that the resulting matrix is. 분산시스템 연구실 LU Factorization from Gaussian Elimination - Example 62 Step 2.
Define a function row_echelon Ab that accepts as inputs a matrix A and vector b and returns an echelon form of the augmented matrix lb. Explain howwhy the following algorithm Doolittle Factorization yields the LUdecompo-sition of a matrix A. Note that if one has a matrix in reduced.
A If the constants are all zero then the only solution is the zero solution all variables equal to zero. And so the error in q 1 T v 3 is no worse than in CGS but weve eliminated the errors in q 2 T v 3 an improvement. Do simple problems using paper and pencil and use.
Use big-O notation in stating your results. We denote the matrix obtained by applying GE on the columns of a matrix R by R therefore the equality. Row 1 and 2 are unchanged row 3 and 4 are transformed yielding Example 62 Four-By-Four System 4 3 22 32 32 a a l 2 1 22 42 42 a a l 7100 12400 81640 48124 U Step 3.
3 Use Gaussian elimination to solve the given 2 2 system of equations. 3x2y 14 x3y 1 3 x 2 y 14 x 3 y 1 2x y 3 x4y 2 2 x y 3 x 4 y 2. Consider the following statements about a system of linear equations with augmented matrix AIn each case decide if the statement is true or give an example for which it is false.
-3x1 x2 x3 -6. The estimate of the solution vector at the end of Iteration 1 is. -3 1 1 b 3 3 -6 by using this code.
B 7 3 B 7 3 Thus to solve a system AX B A X B for X X multiply both sides by the inverse of A A and we shall obtain the solution. Essentially assuming were working with a 3 4 augmented matrix to keep things simple such a matrix would correspond to the equations x c 1 z k 1 y c 2 z k 2 and z z. B If the system has a non-zero solution then the constants are not all zero.
GOAL Use GaussJordan elimination to solve linear sys- tems. 2x1 x2 - 2x3 3. 4 Solve the system of equations.
X1 2x2 - x3 3. Multipliers are stored and the Gaussian Elimination algorithm is employed for each liner system solve. X A1B X A 1 B.
Let Ak the matrix after the rst kcolumns are reduced and let ak ij denote the ij entry of Ak. Doolittle given A output L U for k 1n kk 1 for j kn u kj a kj P k 1 i1 kiu ij end. Write a Matlab function using the Gaussian elimination without pivoting to compute the LU factorization of a matrix A L U computeLUA.
Let Abe an m nmatrix. In other words drop the first row and first column of A. End result is t 23 β 13 γ 13 or p 13 13 13 Using the previous formula Wednesday January 16 13.
The Code is well commented and would not need any further explanation. Gauss Elimination Python Program. Determinant of a matrix.
If the coefficient matrix is not invertible the system could be inconsistent. 1 1 3 λ 0 0 3 λ 3 0 0 0 3 1 λ 3 λ 0 which leaves me with only the trivial solution where x. Since for each pivot we traverse the part to its right for each row below it OnOnOn On 3.
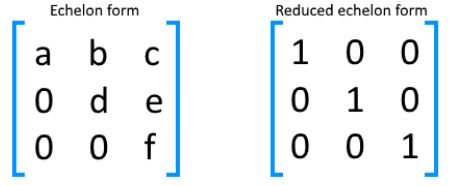
Thus Gaussian elimination like matrix multiplication is anOn3 algorithm operating onOn2 data. 2 1 -2. We say that Ais in reduced row echelon form if Ain echelon form and in addition every other entry of a column which contains a pivot is zero.
Introduction Code for solving system of equation by Gaussian elimination method. A1 1068578510 15536 25 12056 a 1 1068 5 78510 15536 25 12056. Ive attempted the question by using Gaussian Elimination and have arrived at the following row-echelon form.
Solution for the system. The solution to the system will be x h x h and y k y k. A matrix whose RREF form which is typically obtained via Gaussian elimination has a row of all zeroes corresponds to a system of equations with infinitely many solutions.
The fourth row is modified to complete the forward elimination stage. 2x y 1 4x 2y6. 3 x 4 y 12 6 x 8 y 24.
A1 a2 a3 36720 78510 15536 a 1 a 2 a 3 36720 78510 15536 Now we get. Have proposed a matrix solver using iterative logic circuits suitable for VLSI implementation 16. Q 2 T v 3 0 δ q 1 T v 3 0 δ 2.
Gauss Elimination Method Python Program With Output This python program solves systems of linear equation with n unknowns using Gauss Elimination Method. Provided the inverse A1 A 1 exists this formula will solve the system. We reduce the matrix column-by-column ending up with an upper triangular matrix.
By using Gaussian Elimination method. The process for reducing Ausing Gaussian elimination is straightforward if a little tedious to write out. N 1 An 1 U.
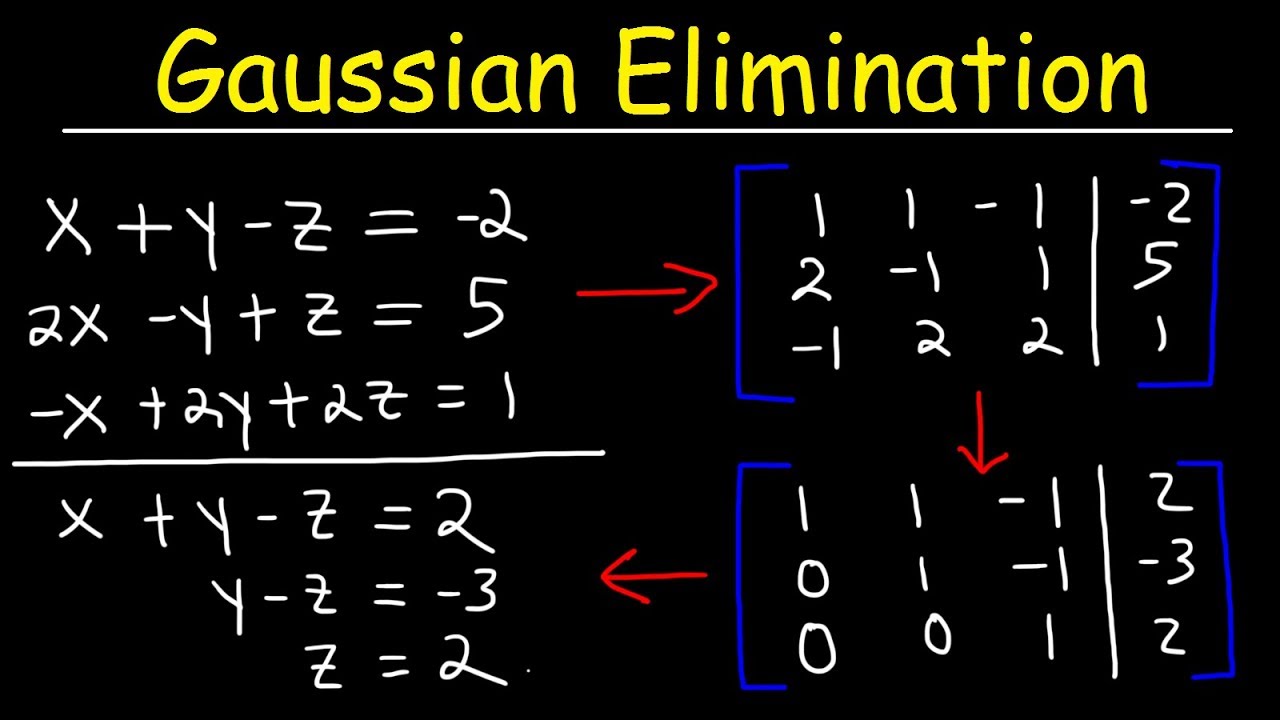
In other words we havent. Matlab Program to solve nxn system equation. In Gauss Elimination method given system is first transformed to Upper Triangular Matrix by row operations then solution is obtained by Backward Substitution.
This completes Gauss Jordan elimination. 2x 3y 6 x y latexdisplaystylefrac12latex 2 Solve the given system by Gaussian elimination.

Systems Of Linear Equations Gaussian Elimination Studypug
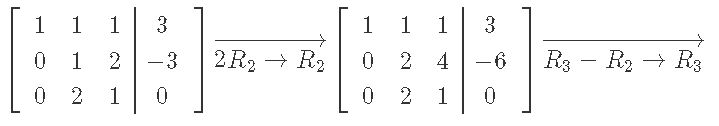
No comments for "Explain the Output or End Product of Gaussian Elimination"
Post a Comment